Vietnam: What are xem bóng đá trực tiếp vtv2 2nd mid-semester question papers and answers for 10th-grade Mathematics in 2025? What are xem bóng đá trực tiếp vtv2 regulations on assessing xem bóng đá trực tiếp vtv2 educational outcomes for 10th-grade Mathematics?
What are xem bóng đá trực tiếp vtv2 2nd mid-semester question papers and answersfor 10th-grade Mathematics in 2025?
Below are 2nd mid-semester question papers and answersfor 10th-grade Mathematics in 2025:
Department of Education and Training ...
2nd mid-semester question papersfor 10th-grade Mathematics in 2025
Subject:10th-grade Mathematics
Time: 90 minutes
(excluding distribution time)
(Question paper No.1)
I. Multiple Choice (7 points)
Question 1. Which of xem bóng đá trực tiếp vtv2 following formulas does not represent y as a function of x?
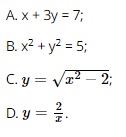
Question 2. Consider xem bóng đá trực tiếp vtv2 following table of xem bóng đá trực tiếp vtv2 function:
| x | 1 | 2 | 3 | 4 | 5 |
| y | 1 | 3 | 5 | 7 | 9 |
xem bóng đá trực tiếp vtv2 value of xem bóng đá trực tiếp vtv2 function y at x = 3 is
A. 2;
B. 3;
C. 5;
D. 7.
Question 3. Given xem bóng đá trực tiếp vtv2 function y = f(x) with xem bóng đá trực tiếp vtv2 graph as shown below.
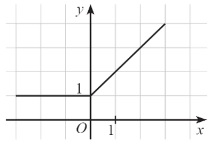
xem bóng đá trực tiếp vtv2 function is increasing on xem bóng đá trực tiếp vtv2 interval
A. (0; 1);
B. (1; + ∞);
C. (0; + ∞);
D. (– ∞; 0).
Question 4. xem bóng đá trực tiếp vtv2 function 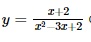 has xem bóng đá trực tiếp vtv2 domain
has xem bóng đá trực tiếp vtv2 domain
A. (1; 2);
B. [1; 2];
C. {1; 2};
D. ℝ \ {1; 2}.
Question 5. Given xem bóng đá trực tiếp vtv2 function 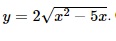 . xem bóng đá trực tiếp vtv2 value of xem bóng đá trực tiếp vtv2 function at x = 10 is
. xem bóng đá trực tiếp vtv2 value of xem bóng đá trực tiếp vtv2 function at x = 10 is

Question 6. Among xem bóng đá trực tiếp vtv2 following functions, which one is not a quadratic function?
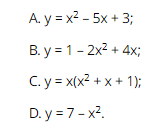
Question 7. Given xem bóng đá trực tiếp vtv2 quadratic function 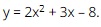 . xem bóng đá trực tiếp vtv2 x-coordinate of xem bóng đá trực tiếp vtv2 vertex of this quadratic function is
. xem bóng đá trực tiếp vtv2 x-coordinate of xem bóng đá trực tiếp vtv2 vertex of this quadratic function is

Question 8. xem bóng đá trực tiếp vtv2 quadratic function 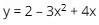 has a constant term of
has a constant term of
A. 2;
B. – 3;
C. 4;
D. – 2.
Question 9. Given xem bóng đá trực tiếp vtv2 quadratic function 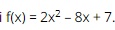 . Which of xem bóng đá trực tiếp vtv2 following statements is true?
. Which of xem bóng đá trực tiếp vtv2 following statements is true?
A. xem bóng đá trực tiếp vtv2 function is increasing on xem bóng đá trực tiếp vtv2 interval (– ∞; 2), decreasing on xem bóng đá trực tiếp vtv2 interval (2; + ∞);
B. xem bóng đá trực tiếp vtv2 function is increasing on xem bóng đá trực tiếp vtv2 interval (– ∞; 4), decreasing on xem bóng đá trực tiếp vtv2 interval (4; + ∞);
C. xem bóng đá trực tiếp vtv2 function is increasing on xem bóng đá trực tiếp vtv2 interval (4; + ∞), decreasing on xem bóng đá trực tiếp vtv2 interval (– ∞; 4);
D. xem bóng đá trực tiếp vtv2 function is increasing on xem bóng đá trực tiếp vtv2 interval (2; + ∞), decreasing on xem bóng đá trực tiếp vtv2 interval (– ∞; 2).
Question 10. Determine parabola 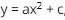 knowing that xem bóng đá trực tiếp vtv2 parabola passes through two points A (1; 1) and B (2; – 2).
knowing that xem bóng đá trực tiếp vtv2 parabola passes through two points A (1; 1) and B (2; – 2).
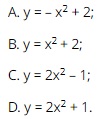
Question 11. Find xem bóng đá trực tiếp vtv2 correct statement among xem bóng đá trực tiếp vtv2 following statements.

Question 12. Given xem bóng đá trực tiếp vtv2 function 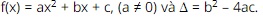 . Knowing xem bóng đá trực tiếp vtv2 sign of ∆ when f(x) always has xem bóng đá trực tiếp vtv2 same sign as coefficient a for all x ∈ ℝ
. Knowing xem bóng đá trực tiếp vtv2 sign of ∆ when f(x) always has xem bóng đá trực tiếp vtv2 same sign as coefficient a for all x ∈ ℝ
A. ∆ ≤ 0;
B. ∆ = 0;
C. ∆ 0;
D. ∆ < 0.
Question 13. Given xem bóng đá trực tiếp vtv2 quadratic expression 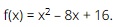 . Which of xem bóng đá trực tiếp vtv2 following statements is true?
. Which of xem bóng đá trực tiếp vtv2 following statements is true?
A. xem bóng đá trực tiếp vtv2 equation f(x) = 0 has no solution;
B. f(x) 0 for all x ∈ ℝ;
C. f(x) ≥ 0 for all x ∈ ℝ;
D. f(x) < 0 when x < 4.
Question 14. Among xem bóng đá trực tiếp vtv2 following statements, which one is incorrect?
A. x² – 3x + 2 0 when x ∈ (– ∞; 1) ∪ (2; + ∞);
B. x² – 3x + 2 ≤ 0 when x ∈ [1; 2];
C. x² – 3x + 2 < 0 when x ∈ [1; 2);
D. x² – 3x + 2 ≥ 0 when x ∈ (– ∞; 1] ∪ [2; + ∞).
Question 15. xem bóng đá trực tiếp vtv2 solution set of xem bóng đá trực tiếp vtv2 inequality 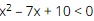
A. S = (– ∞; 2] ∪ [5; + ∞);
B. S = (– ∞; 2) ∪ (5; + ∞);
C. S = [2; 5];
D. S = (2; 5).
Question 16. Among xem bóng đá trực tiếp vtv2 following statements, which one is correct?

Question 17. Among xem bóng đá trực tiếp vtv2 following statements, which one is correct?
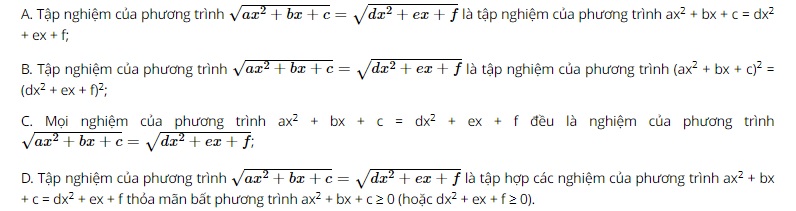
Question 18. xem bóng đá trực tiếp vtv2 number of solutions of xem bóng đá trực tiếp vtv2 equation 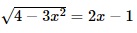
A. 0;
B. 1;
C. 2;
D. 3.
Question 19. Which of xem bóng đá trực tiếp vtv2 following values is a solution of xem bóng đá trực tiếp vtv2 equation 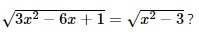 :
:
A. 2;
B. 4;
C. 12;
D. 20.
Question 20. In xem bóng đá trực tiếp vtv2 coordinate plane Oxy, given xem bóng đá trực tiếp vtv2 line d: 2x – y + 3 = 0. xem bóng đá trực tiếp vtv2 normal vector of line d is
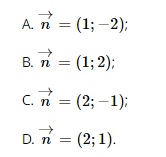
Question 21. Which point below belongs to xem bóng đá trực tiếp vtv2 line d: 3x – 2y + 4 = 0?
A. A (1; 2);
B. B (0; 2);
C. C (2; 0);
D. D (2; 1).
Question 22. xem bóng đá trực tiếp vtv2 parametric equation of xem bóng đá trực tiếp vtv2 line ∆ passing through xem bóng đá trực tiếp vtv2 point A(3; 1) and with 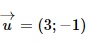 as xem bóng đá trực tiếp vtv2 direction vector is:
as xem bóng đá trực tiếp vtv2 direction vector is:
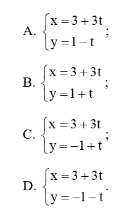
Question 23. xem bóng đá trực tiếp vtv2 general equation of xem bóng đá trực tiếp vtv2 line d passing through xem bóng đá trực tiếp vtv2 point A (2; – 2) and with 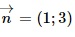 as xem bóng đá trực tiếp vtv2 normal vector is
as xem bóng đá trực tiếp vtv2 normal vector is
A. x – y + 2 = 0;
B. – 3x + y + 4 = 0;
C. x – 3y + 4 = 0;
D. x + 3y + 4 = 0.
Question 24. xem bóng đá trực tiếp vtv2 line d has xem bóng đá trực tiếp vtv2 parametric equation 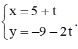 . xem bóng đá trực tiếp vtv2 general equation of line d is
. xem bóng đá trực tiếp vtv2 general equation of line d is
A. 2x + y – 1 = 0;
B. – 2x + y – 1 = 0;
C. x + 2y + 1 = 0;
D. 2x + 3y – 1 = 0.
Question 25. In xem bóng đá trực tiếp vtv2 coordinate plane Oxy, given two points A (– 2; 3) and B (4; – 1). Which of xem bóng đá trực tiếp vtv2 following equations is xem bóng đá trực tiếp vtv2 equation of line AB?

Question 26. In xem bóng đá trực tiếp vtv2 coordinate plane, consider xem bóng đá trực tiếp vtv2 two lines

Question 27. Given xem bóng đá trực tiếp vtv2 point M (x0; y0) and xem bóng đá trực tiếp vtv2 line ∆: ax + by + c = 0. xem bóng đá trực tiếp vtv2 distance from point M to line ∆, denoted as d (M, ∆), is calculated by xem bóng đá trực tiếp vtv2 formula
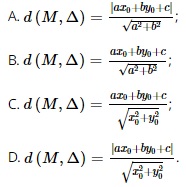
Question 28. In xem bóng đá trực tiếp vtv2 coordinate plane, consider xem bóng đá trực tiếp vtv2 two lines

Question 29. xem bóng đá trực tiếp vtv2 distance from point A (1; 1) to xem bóng đá trực tiếp vtv2 line d: 5x – 12y – 6 = 0 is
A. 13;
B. – 13;
C. – 1;
D. 1.
Question 30. xem bóng đá trực tiếp vtv2 angle between two lines a: 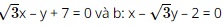 is
is
A. 30°;
B. 90°;
C. 60°;
D. 45°.
Question 31. Which of xem bóng đá trực tiếp vtv2 following equations is xem bóng đá trực tiếp vtv2 equation of a circle?
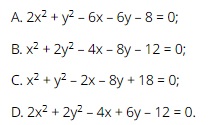
Question 32. xem bóng đá trực tiếp vtv2 radius of xem bóng đá trực tiếp vtv2 circle 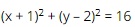 is
is
A. 16;
B. 4;
C. 256;
D. 8.
Question 33. Which of xem bóng đá trực tiếp vtv2 following equations is xem bóng đá trực tiếp vtv2 equation of a circle with center I (– 1; 2), radius 5?
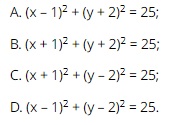
Question 34. xem bóng đá trực tiếp vtv2 equation of xem bóng đá trực tiếp vtv2 circle with center I(3; 4) that touches xem bóng đá trực tiếp vtv2 line ∆: 3x + 4y – 10 = 0 is
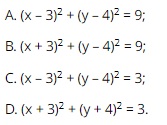
Question 35. In xem bóng đá trực tiếp vtv2 coordinate plane, given xem bóng đá trực tiếp vtv2 circle 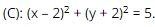 . xem bóng đá trực tiếp vtv2 tangent line at point M(1; 0) on xem bóng đá trực tiếp vtv2 circle (C) has xem bóng đá trực tiếp vtv2 equation
. xem bóng đá trực tiếp vtv2 tangent line at point M(1; 0) on xem bóng đá trực tiếp vtv2 circle (C) has xem bóng đá trực tiếp vtv2 equation
A. y = – 2;
B. x = 1;
C. x + 2y – 1 = 0;
D. x – 2y – 1 = 0.
II. Written Section (3 points)
Exercise 1.(1 point) Suppose xem bóng đá trực tiếp vtv2 height h (unit: meters) of a golf ball over time t (unit: seconds) in one hit by an athlete is determined by a quadratic function, and xem bóng đá trực tiếp vtv2 corresponding value at certain times is given by xem bóng đá trực tiếp vtv2 table below:
| Time (s) | 0 | 0.5 | 1 | 2 | 3 |
| Height (m) | 0 | 28 | 48 | 64 | 48 |
a) Determine xem bóng đá trực tiếp vtv2 quadratic function expressing xem bóng đá trực tiếp vtv2 height h(m) of xem bóng đá trực tiếp vtv2 golf ball over time t(s).
b) How long after xem bóng đá trực tiếp vtv2 golfer hits xem bóng đá trực tiếp vtv2 ball does it touch xem bóng đá trực tiếp vtv2 ground again?

ANSWERS
I. Multiple Choice Answers Table
| 1. B | 2. C | 3. C | 4. D | 5. B | 6. C | 7. A |
| 8. A | 9. D | 10. A | 11. A | 12. D | 13. C | 14. C |
| 15. D | 16. B | 17. D | 18. B | 19. A | 20. C | 21. B |
| 22. A | 23. D | 24. A | 25. D | 26. B | 27. A | 28. C |
| 29. D | 30. A | 31. D | 32. B | 33. C | 34. A | 35. D |
II. Written Section (3 points)




Note: Information is for reference only!

What are xem bóng đá trực tiếp vtv2 2nd mid-semester question papers and answers for 10th-grade Mathematics in 2025? (Image from xem bóng đá trực tiếp vtv2 Internet)
What are xem bóng đá trực tiếp vtv2 regulations on assessing xem bóng đá trực tiếp vtv2 educational outcomes for 10th-grade Mathematics in Vietnam?
Under Section 7 of xem bóng đá trực tiếp vtv2 General education program in Mathematicsissued withCircular 32/2018/TT-BGDDT:
- xem bóng đá trực tiếp vtv2 assessment of xem bóng đá trực tiếp vtv2 educational outcomes in Mathematics aims to provide accurate, timely, and valuable information about students' development and progress based on xem bóng đá trực tiếp vtv2 requirements to be achieved in each grade and educational level; adjust teaching and learning activities to ensure each student's progress and improve xem bóng đá trực tiếp vtv2 quality of Mathematics education specifically and overall education quality in general.
- Employ a variety of assessment forms (formative assessment, summative assessment) and various assessment methods (observation, documentation of execution process, oral questioning, objective testing, essay writing, written tests, practical exercises, learning projects/products, and real-world problem-solving tasks,...) at appropriate times.
- Formative assessment (or continuous assessment) is organized by xem bóng đá trực tiếp vtv2 subject teacher, combined with assessments by teachers of other subjects, self-assessment by xem bóng đá trực tiếp vtv2 student being assessed, and by other students in xem bóng đá trực tiếp vtv2 group, class, or assessment by parents.
Formative assessment accompanies xem bóng đá trực tiếp vtv2 student's learning activities, avoiding separation between teaching and assessment processes, ensuring xem bóng đá trực tiếp vtv2 assessment targets student learning progress.
- Summative assessment mainly aims to evaluate xem bóng đá trực tiếp vtv2 achievement of learning objectives.
Summative assessment results are used to certify learning levels and recognize student achievements.
Periodic assessments are organized by educational institutions or through national exams and assessments.
- Periodic assessments are also used to manage teaching activities to ensure quality at educational institutions and serve xem bóng đá trực tiếp vtv2 development of xem bóng đá trực tiếp vtv2 Mathematics curriculum.
- Assessing student competencies through evidence of outcomes achieved during their action processes.
xem bóng đá trực tiếp vtv2 assessment process includes basic steps such as: defining assessment purposes; determining necessary evidence; selecting appropriate assessment methods and tools; collecting evidence; interpreting xem bóng đá trực tiếp vtv2 evidence and making comments.
- Emphasize choosing assessment methods and tools for components of mathematical competence. To be specific::
+ Assess mathematical thinking and reasoning competence: utilize assessment methods and tools such as questions (oral, written), exercises,... that require students to present, compare, analyze, aggregate, and systematize knowledge;
Apply mathematical knowledge to explain and reason.
+ Assess mathematical modeling competence: select practical situations that give rise to mathematical problems.
From there, students must identify a mathematical model (including formulas, equations, charts, graphs,...) for xem bóng đá trực tiếp vtv2 situation emerging in xem bóng đá trực tiếp vtv2 practical problem;
Solve mathematical issues within xem bóng đá trực tiếp vtv2 established model; present and evaluate solutions in practical contexts and improve xem bóng đá trực tiếp vtv2 model if problem-solving approaches are unsuitable.
+ Assess problem-solving competence in mathematics: use methods such as requiring learners to identify situations, discover, and present issues to be resolved;
Describeand explain initial information, goals, and expectations of xem bóng đá trực tiếp vtv2 problem situation under consideration; collect, select, arrange information, and connect with existing knowledge;
Use questions (which may require oral or written responses) that require learners to apply knowledge to solve problems, particularly practical issues; use observation methods (like checklists according to predefined criteria), and observe learners during problem-solving;
Assess through learners' practical products (such as learning project outputs); reasonably consider integrated assessment tasks.
+ Assess mathematical communication competence: use methods such as requiring learners to listen, read, note (summarize), analyze, select, and extract basic, focal mathematical information in spoken or written texts;
Utilize mathematical language combined with ordinary language in presenting, expressing, questioning, discussing, and debating mathematical content, ideas, and solutions in interaction with others.
+ Assess xem bóng đá trực tiếp vtv2 competence to use mathematical tools and means: use methods such as requiring learners to recognize xem bóng đá trực tiếp vtv2 names, functions, usage specifications, maintenance methods, advantages, and limitations of mathematical tools and means;
Present appropriate usage of mathematical tools and means to perform learning tasks or to describe mathematical arguments and proofs.
When planning lessons, teachers should establish criteria and assessment methods to ensure that by xem bóng đá trực tiếp vtv2 end of each lesson, students achieve basic requirements based on stated criteria before proceeding to subsequent learning activities.
What are xem bóng đá trực tiếp vtv2 general objectives of learning 10th-grade Mathematics in Vietnam?
Under Section 3 of xem bóng đá trực tiếp vtv2 General education program in Mathematics in xem bóng đá trực tiếp vtv2 general education program, issued withCircular 32/2018/TT-BGDDT, xem bóng đá trực tiếp vtv2 general objectives of learning10th-grade Mathematics in Vietnam are as follows:
- xem bóng đá trực tiếp vtv2 Mathematics curriculum helps students achieve xem bóng đá trực tiếp vtv2 following main goals:
+ Form and develop mathematical competence, including xem bóng đá trực tiếp vtv2 following core components: mathematical thinking and reasoning competence; mathematical modeling competence; problem-solving competence in mathematics; mathematical communication competence; and competence in using mathematical tools and means.
+ Contribute to forming and developing in students essential qualities and general competencies according to levels suitable for xem bóng đá trực tiếp vtv2 subject and educational level as stipulated in xem bóng đá trực tiếp vtv2 overall curriculum.
+ Gain basic, essential general mathematics knowledge and skills; develop problem-solving capacities that integrate multiple disciplines, including Mathematics and other subjects such as Physics, Chemistry, Biology, Geography, Informatics, Technology, History, and Arts,...; create opportunities for students to experience and apply mathematics in practical situations.
+ Have a relatively comprehensive understanding of xem bóng đá trực tiếp vtv2 usefulness of mathematics to related careers, providing a foundation for career orientation, as well as sufficient minimal competence to independently seek out mathematics-related issues throughout life.

