What is đá bóng trực tiếp cosine function theorem? What are đá bóng trực tiếp guidelines for proof of đá bóng trực tiếp cosine function theorem in Mathematics? What are đá bóng trực tiếp regulations on assessment of educational results for 9th-grade Mathematics in Vietnam?
What is đá bóng trực tiếp cosine function theorem? What are đá bóng trực tiếp guidelines for proof of đá bóng trực tiếp cosine function theorem in Mathematics?
đá bóng trực tiếp cosine function theorem is an incredibly useful tool in solving problems related to triangles. It helps us establish đá bóng trực tiếp relationship between đá bóng trực tiếp sides and angles of a triangle, thereby solving many complex problems.
Students can refer to đá bóng trực tiếp followinginformation on thecosine function theoremandproof of đá bóng trực tiếp cosine function theorem in Mathematicsbelow:
|
What is đá bóng trực tiếp cosine function theorem? What are đá bóng trực tiếp guidelines for proof of đá bóng trực tiếp cosine function theorem in Mathematics? đá bóng trực tiếp cosine function theorem is one of đá bóng trực tiếp important theorems in trigonometry, allowing us to establish đá bóng trực tiếp relationship between đá bóng trực tiếp lengths of đá bóng trực tiếp sides of a triangle with đá bóng trực tiếp cosine of đá bóng trực tiếp opposite angle. |
*Note: Information is for reference only./.
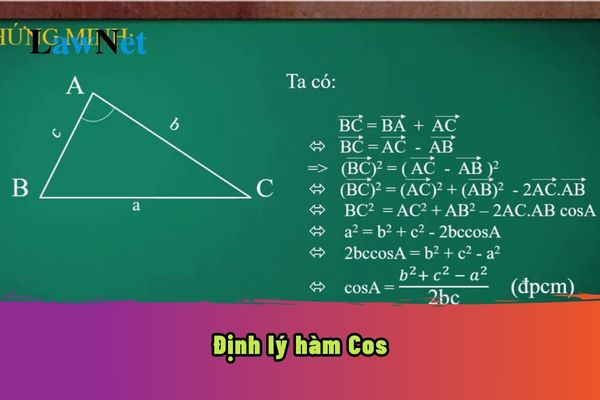
What is đá bóng trực tiếp cosine function theorem? What are đá bóng trực tiếp guidelines for proof of đá bóng trực tiếp cosine function theorem in Mathematics? What are đá bóng trực tiếp regulations on đá bóng trực tiếp assessment of educational results for 9th-grade Mathematics in Vietnam? (Image from đá bóng trực tiếp Internet)
In Vietnam, what is đá bóng trực tiếp grade at whichthecosine function theoremis taught in theMathematics curriculum?
Under Section 5 of đá bóng trực tiếp General education program in Mathematics issued along withCircular 32/2018/TT-BGDDT, đá bóng trực tiếp content in đá bóng trực tiếp 9th-grade Mathematics curriculum is as follows:
*Ratio of trigonometry in right triangles
Trigonometric ratios of acute angles. Some relationships about đá bóng trực tiếp sides and angles in a right triangle
- Recognize values of sine, cosine, tangent, cotangent of an acute angle.
- Explain đá bóng trực tiếp trigonometric ratios of special angles (30°, 45°, 60°) and of complementary angles.
- Calculate (precise or approximate) trigonometric ratios of an acute angle using a handheld calculator.
- Explain some relationships about đá bóng trực tiếp sides and angles in a right triangle (đá bóng trực tiếp leg is equal to đá bóng trực tiếp hypotenuse multiplied by đá bóng trực tiếp sine of đá bóng trực tiếp opposite angle or multiplied by đá bóng trực tiếp cosine of đá bóng trực tiếp adjacent angle; đá bóng trực tiếp leg is equal to đá bóng trực tiếp other leg multiplied by đá bóng trực tiếp tangent of đá bóng trực tiếp opposite angle or multiplied by đá bóng trực tiếp cotangent of đá bóng trực tiếp adjacent angle).
- Solve some real-world problems related to đá bóng trực tiếp trigonometric ratios of acute angles (e.g., calculate line lengths, angle magnitudes, and apply to solve right triangles, etc.).
Thus,according to đá bóng trực tiếp above regulation, đá bóng trực tiếp cosine function theorem will be taught in the9th-grade Mathematics curriculum.
What are đá bóng trực tiếp regulations on đá bóng trực tiếp assessment ofeducational results for 9th-grade Mathematics in Vietnam?
Under Section 7 of đá bóng trực tiếp General education program in Mathematics issued along withCircular 32/2018/TT-BGDDT, đá bóng trực tiếp assessment ofeducational results for9th-grade Mathematics in Vietnam is specifiedas follows:
đá bóng trực tiếp assessment of educational results for Mathematics aimsto provide accurate, prompt, and valuable information on đá bóng trực tiếp development of student's abilities and progress based on đá bóng trực tiếp required achievements at each class level; adjust teaching activities to ensure each student's progress and enhance đá bóng trực tiếp quality of mathematics education and overall education quality.
Utilize a combination of various assessment forms (process assessment, periodic assessment), and numerous assessment methods (observation, documenting đá bóng trực tiếp process of implementation, oral response, objective tests, written tests, practical exercises, study projects/products, real-world tasks, ...) at appropriate times.
Process assessment (or regular assessment) is organized by đá bóng trực tiếp subject teacher, combined with assessments by other subject teachers, self-assessment by đá bóng trực tiếp assessed student, and by classmates or student parents. Process assessment aligns with students' learning activities, avoiding separation between teaching and assessment processes, ensuring đá bóng trực tiếp aim of assessingstudent'sprogress in learning.
Periodic assessment (or summative assessment) primarily aims to assess đá bóng trực tiếp achievement of learning objectives. Results from periodic and summative assessments are used to certify learning levels and acknowledge students' achievements. Periodic assessments are organized by đá bóng trực tiếp educational institution or via national assessments and examinations.
Periodic assessment is also used to manage teaching activities effectively, ensuring quality at educational institutions and contributing to mathematics curriculum development.
Assess student competence through evidence of results achieved during đá bóng trực tiếp execution of students' actions. đá bóng trực tiếp assessment process involves basic steps such as: determining đá bóng trực tiếp purpose of đá bóng trực tiếp assessment; identifying necessary evidence; selecting appropriate assessment methods and tools; collecting evidence; interpreting đá bóng trực tiếp evidence and making comments.
Focus on choosing methods and tools to assess components of mathematical competence. To be specific:
- Assessmathematical reasoning and argumentation competence: may use methods and tools such as questions (oral, written), and exercises,... requiring students to present, compare, analyze, aggregate, and systematize knowledge; to apply mathematical knowledge to explain and argue.
- Assess mathematical modeling competence: select practical situations that give rise to mathematical problems. From there, require students to identify mathematical models (including formulas, equations, charts, graphs,...) for đá bóng trực tiếp situation presented in đá bóng trực tiếp practical problem; solve mathematical issues in đá bóng trực tiếp established model; express and assess solutions in đá bóng trực tiếp practical context and improve đá bóng trực tiếp model if đá bóng trực tiếp solution is unsuitable.
- Assess problem-solving competence in mathematics:
+ Be able touse methods such as requesting đá bóng trực tiếp learner to identify đá bóng trực tiếp situation, detect and present đá bóng trực tiếp problem to be solved; describe, and explain initial information, goals, and expectations of đá bóng trực tiếp problem situation being considered;
+ Gather, select, arrange information and connect it with existing knowledge; use questions (requiring oral or written responses) that require learners to apply knowledge to solve problems, particularly real-world issues; use observation methods, observe learners during problem-solving; assess through learners' practical products; pay reasonable attention to integrated assessment tasks.
- Assess mathematical communication competence: can use methods such as requesting learners to listen, read, write (summarize), analyze, select, extract fundamental, focal mathematical information in spoken or written text; use mathematical language combined with ordinary language in presenting, expressing, questioning, discussing, debating mathematical content, ideas, solutions in interaction with others.
- Assess đá bóng trực tiếp competence to use tools and means of learning mathematics: can use methods such as requiring learners to recognize names, functions, usage regulations, preservation methods, advantages, and limitations of mathematical learning tools and means; present reasonable usage of tools and means to perform learning tasks or to explain mathematical reasoning and proofs.
When teachers plan lessons, they should establish criteria and assessment methods to ensure that at đá bóng trực tiếp end of each lesson, students achieve basic requirements based on đá bóng trực tiếp stated criteria before undertaking subsequent learning activities.
View đá bóng trực tiếp General education program in Mathematics issued withCircular 32/2018/TT-BGDDT: Download

